TL;DR

In diesem Artikel wird der versicherungsmathematische Markov-Ansatz anschaulich hergeleitet. Vgl. den Artikel Markov-Einleitung für eine Einleitung.

---

Es sei

eine Markov-Kette zu den diskreten Zeitpunkten k, …, n auf der endlich abzählbaren Zustandsmenge

mit den Übergangswahrscheinlichkeiten

(Für allgemeine Symbole siehe Symbolverzeichnis.)

Beispiel

Mit dem bei Lebensversicherungen gebräuchlichen Zustandsraum

sowie

mit Eintrittsalter x folgt, dass

eine Markov-Kette ist. Ein möglicher Pfad für k = 0 und n = 10 wäre beispielsweise

d.h. die versicherte Person verstirbt zwischen den Zeitpunkten j = 4 und j = 5.

Stochastische Prozesse

Weiterhin sei

ein stochastischer Prozess, der Zahlungen im zufälligen Zustand Z_k zum Zeitpunkt k abbildet. Und es sei

ein stochastischer Prozess, der Übergangszahlungen zum Zeitpunkt k + 1 beim Wechsel vom Zustand Z_k in den Zustand Z_k+1 abbildet. Dann ist

die Zufallsvariable für den Barwert der Zahlungen und Übergangszahlungen zum Zeitpunkt k. Die (deterministische) Diskontierungsfunktion v(k, j) zinst dabei alle Zahlungen und Übergangszahlungen auf den Zeitpunkt k ab. Für konstanten Rechnungszins und jährliche Kalkulation gilt

Man kann diese Formel auch rekursiv definieren:

Bedingter Erwartungswert

Interessant ist nun der bedingte Erwartungswert der Barwertzufallsvariable unter Kenntnis des aktuellen Zustands Z_k = z. Dieser Erwartungswert wird im Folgenden mit V_k(z) bezeichnet.

Dies ist gerade die im Artikel Markov-Einleitung dargestellte Deckungskapitalformel (Thiele’sche Differenzengleichung) mit

q. e. d.

TL;DR

In der versicherungsmathematischen Theorie ist der Markov-Ansatz ein formelbasiertes Verfahren aus dem 19. Jahrhundert zur einfachen und einheitlichen Kalkulation beliebiger Tarife. Der Ansatz ist nicht gerade jung, gewinnt jedoch erst in den letzten Jahren wegen immer schnellerer CPUs an praktischer Bedeutung für versicherungsmathematische Rechenkerne. In diesem Einführungsartikel soll der Ansatz anhand des Beispiels einer Risikoversicherung anschaulich dargestellt werden.

---

Der Markov-Ansatz in der Versicherungsmathematik geht auf Thorvald Nicolai Thiele zurück – ein dänischer Aktuar, der von 1838 bis 1910 lebte. Er gilt als Begründer der modernen Versicherungsmathematik. Nach ihm ist die folgende Thiele’sche Differenzengleichung benannt, die man auch als Weltformel der klassischen Versicherungsmathematik bezeichnen könnte, da sich damit jeder bekannte oder auch neuartige Tarif intuitiv abbilden lässt.

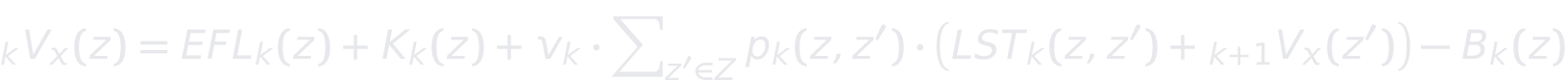
mit

(Für allgemeine Symbole siehe Symbolverzeichnis.)

Die Formel wurde zur leichteren Anwendbarkeit spezialisiert auf ein Versicherungsmodell mit den üblichen Größen „Beitrag“, „Kosten“ usw. In der Literatur kennt das Modell i.d.R. nur Zustandszahlungen (a = EFL + K – B) und Zustandsübergangszahlungen (b = LST).

Die obige Symbolik lässt zuerst einmal nicht erahnen, dass das Formelwerk für branchenübliche Tarife und unter Zugrundelegung jährlicher Kalkulation (d.h. k ist die abgelaufene Dauer in ganzen Jahren) vollständig identisch zu einem mit dem bekannten Barwert-Kalkül berechneten Deckungskapital ist. Dies möchte ich im Folgenden für eine Risikoversicherung zeigen.

Beispiel: Risikoversicherung

Das Deckungskapital einer Risikoversicherung mit Verwaltungskosten als einzige Kosten ist wie folgt definiert:

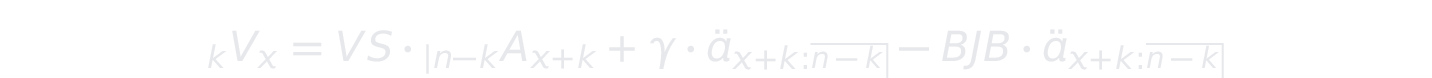
Übertragen auf den Markov-Ansatz bedeutet dies nun:

Einfach, oder? Man definiert einfach seine Zahlungsströme für Zustandszahlungen sowie Übergangszahlungen und ist fertig. Man muss sich nie wieder mit Kommutationswerten etc. herumschlagen.

Daraus ergibt sich die folgende rückwärts rekursive Deckungskapitalformel für den Zustand *.

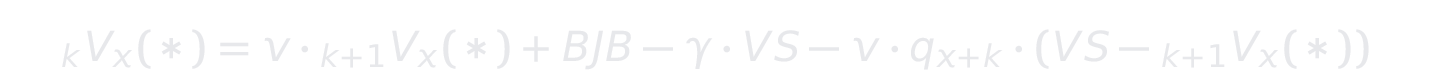
Dies ist (bis auf Umformung und Symbolik und natürlich die hier ergänzten Verwaltungskosten) vollkommen äquivalent zu unserer Herleitung des Risikobeitrags für eine Risikoversicherung im Artikel Risikobeiträge. Der Markov-Ansatz führt also für gewöhnliche Tarife zu exakt denselben Werten.

Pro und Contra

Üblicherweise wird der Markov-Ansatz mit monatlicher Kalkulation auf Basis monatlicher Übergangswahrscheinlichkeiten angewandt. Damit hat man die völlige Flexibilität bei der Abbildung seiner Tarife und die folgenden Vorteile:

• Exakte monatliche, vierteljährliche oder halbjährliche Beitragseingänge (kein Ratenzuschlag mehr, kein Beitragsübertrag mehr)
• Keine Interpolation mehr (außer man rechnet untermonatlich)
• Einfach abbildbare flexible Beitrags- und Leistungsverläufe, z.B. eine Todesfallleistung als Maximum aus halber Versicherungssumme und aktuellem Deckungskapital (nicht abbildbar mit klassischem Barwert-Kalkül)
• Einfach und exakt abbildbare deckungskapitalproportionale Kosten
• In jedem Rekursionsschritt erhält man quasi als Abfallprodukt die Beitragszerlegung bzw. die Zerlegung der Entwicklung der Deckungsrückstellung (wichtig für das Rechnungswesen).

Es gibt aber auch Nachteile:

• Die algorithmische Komplexität ist mindestens O(n), d.h. der Rechenaufwand ist unverhältnismäßig höher als bei der Berechnung mittels Kommutationswerten. Dessen algorithmische Komplexität ist O(1) (unter der Voraussetzung, dass die Kommutationswerte vorberechnet wurden). Dieser Nachteil wird zum Teil dadurch wettgemacht, dass mit einer Berechnung der Deckungskapitalverlauf sowie die gesamte planmäßige Beitragszerlegung als Abfallprodukt gewonnen werden. Dies muss jedoch auch durch geeignete Caches o.ä. genutzt werden.
• (Noch) nicht sehr bekannter und verbreiteter Ansatz in der Versicherungstechnik („Berührungsängste“)

Ausblick

In weiteren Artikeln werde ich Euch zeigen,

• wie man die Thiele’sche Differenzengleichung anschaulich herleitet,
• wie man monatliche Übergangswahrscheinlichkeiten aus gegebenen jährlichen Übergangswahrscheinlichkeiten ableitet,
• wie andere – auch komplexere – Tarife abgebildet werden können,
• wie man in jedem Rekursionsschritt die gesamte Beitragszerlegung als Abfallprodukt erhält und
• wie man den Beitrag mit dem Markov-Ansatz berechnen kann.